RL with Competitive Ensembles of Information-Constrained Primitives
What it says
In hierarchical RL, a policy is decomposed into high-level “meta-policy” and low-level “sub-policies.” In this setting, the low-level sub-policies can specialize in small parts of the task, and the high-level master policy decides when to activate a certain sub-policy. Although such hierarchy might allow for better exploration and generalization, it still relies entirely on the high-level master policy to make a decision.
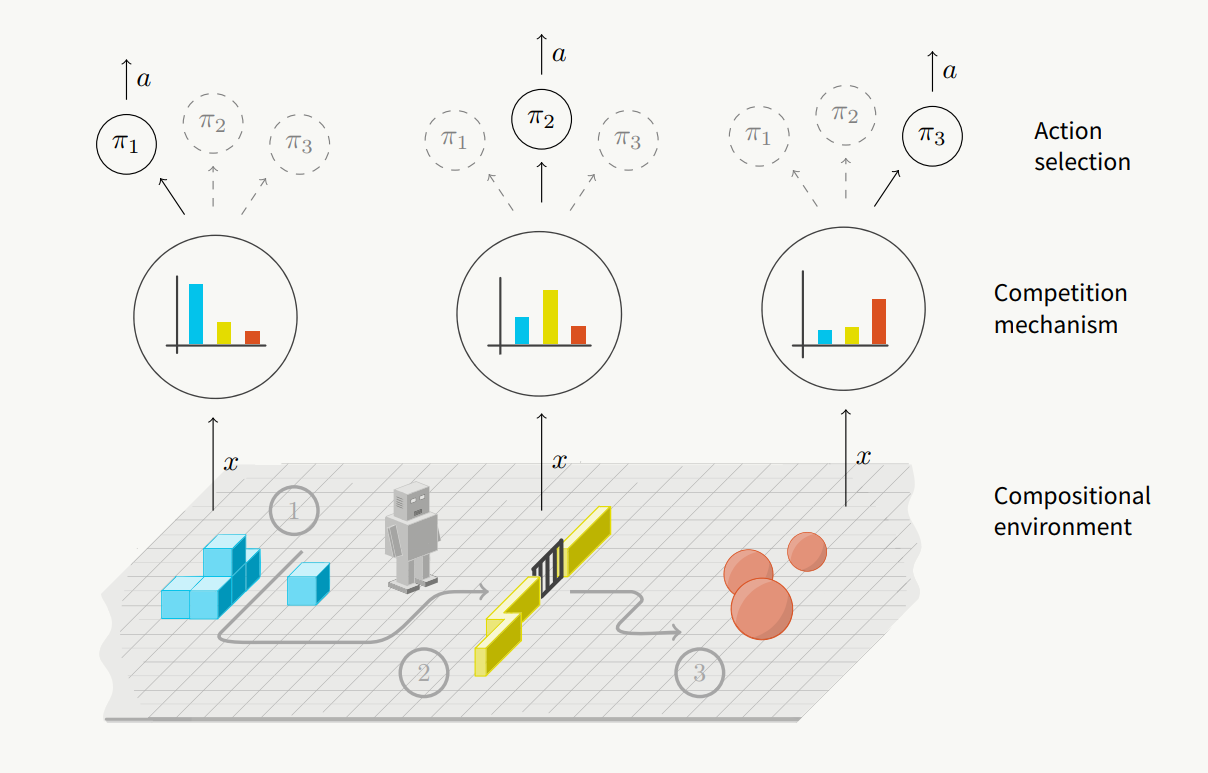
Instead of this centralized decision system, the authors propose a decentralized design that does not have a high-level meta-policy. Instead of a high-level policy that decides for every low-level primitive, in their proposed system, each primitive decide whether it wishes to act or not given a particular situation by competing with one another.
Each primitive is composed of an encoder and a decoder. The encoder is given a state and is meant to output a “good representation” of the state - a representation that contains the information needed for the primitive to perform well on this state. The decoder is given this encoded output and outputs a distribution over the actions. The “information cost” is calculated by a KL-divergence of encoder output and the prior (which is a normal distribution) (Section 3.1). From these primitives, one primitive is chosen either deterministically or stochastically by comparing their information costs.
The competition between these primitives emerge from how the rewards are distributed among primitives. The reward of each primitive is weighted by its “selection coefficient”, which is computed by applying softmax to information cost of all primitives. Thus, “a primitive gets a higher reward for accessing more information about the current state, but that primitive also pays the price (equal to information cost) for accessing the state information” (Section 3.2). To further encourage diversity, the authors also add a regularization term that encourages multiple primitives being used (Section 3.3).
The authors test their algorithm against three baselines: 1) Option Critic, 2) Meta-Learning Shared Hierarchy (MLSH), and 3) Transfer A2C. In a 2D environment Minigrid and continuous control biped environment, this new framework is shown to perform better than these baselines.
Read more
Deep Conservative Policy Iteration
What it says
The problem of reinforcement learning is formalized through Markov Decision Processes (MDPs) with states, actions, rewards, and transition probabilities. Approximate Policy Iteration (API) is among the few approximate dynamic programming (ADP) techniques that are commonly used to solve such MDPs, where a random policy is gradually improved through continued policy evaluation and policy improvement. Conservative Policy Iteration (CPI) is an extension of PI that computes a stochastic mixture of all previous greedy policies. Despite the strong theoretical guarantees, CPI has only been used for small problems with linear function approximators (Section 3.1).
Thus, the authors propose Deep CPI (DCPI), approximating the value function and policy through a neural network. Similar to Deep Q-Networks, both the Q-network and the policy network has an online network and a target network (Section 4). Due to such similarity, DCPI is an extension of DQN, since DCPI can be reduced to DQN or Double DQN under some assumptions.
The authors also compare different mixture rates for mixing greedy policies in CPI The authors show that in CartPole, a constant mixture rate with a small learning rate results in a stable but slow learning, and increasing the learning rate improves speed at the cost of stability (Section 6.1). Thus, the authors propose using adaptive mixture rates.
The authors test DCPI on 20 Atari environments and compare its results with DQN. DCPI outperforms DQN in some environments but also achieves lower score on other environments (Figure 4, 6).
Read more
External resources
- Reinforcement Learning: An Introduction - 4.3 Policy Iteration: A nice resource for PI
- Approximately Optimal Approximate Reinforcement Learning (PDF): Introduced CPI
Optimistic Proximal Policy Optimization
What it says
Optimism in the face of uncertainty (OFU) principle has been known to be a effective way to encourage exploration. Based on this concept, O’Donoghue et al. derived the Uncertainty Bellman Equation (UBE) that allows the propagation of uncertainty over Q-values across multiple time steps, and showed that it can be used to improved the performance of Deep Q-Networks (DQNs) on the Atari testbed.
The authors propose applying the idea of UBE to Proximal Policy Optimization (PPO) and call it Optimistic Proximal Policy Optimization (OPPO)(Section 3). For computing the uncertainty, the authors use the Random Network Distillation (RND) bonus by Burda et al. (This makes OPPO very similar to RND). Tested on 6 Atari Hard environments (Frostbite, Freeway, Solaris, Venture, Montezuma’s Revenge, and Private Eye), OPPO shows performance competitive to RND.
Read more
External resources
- The Uncertainty Bellman Equation and Exploration (ArXiv Preprint): Introduced UBE
- Proximal Policy Optimization Algorithms (ArXiv Preprint): Introduced PPO
- Exploration by Random Network Distillation (ArXiv Preprint): Introduced RND
More exciting news in RL:
- OpenAI released OpenAI Remote Rendering Backend (ORRB), a customizable robotics renderer.
- Lilian Weng wrote a blog post on Meta RL.
- DeepMind proposed methods of training expressive generative models with stable belief-states, which can be used to train model-based agents at a level competitive to model-free counterparts.
- Zhang et al. proposed methods of learning task-agnostic causal state representations from POMDPs.